Nachdem im vorhergehenden Statik-Skript der Begriff Moment bzw. Drehmoment erläutert wurde, folgen hier nun einige Beispiele und Übungsaufgaben.
Beispiel 1 – waagrechter Stab
Wie man im Bild unten sehen kann, liegt in dieser Übungsaufgabe ein waagrechter Stab vor, der an einer Stelle drehbar gelagert ist. An den beiden Enden des Stabes setzten die Kräfte F1 und F2 an. Das System befindet sich im Gleichgewicht; d.h. der Stab bewegt sich nicht.
Die beiden Kräfte verursachen über ihren jeweiligen Hebelarm (L1 bzw. L2) auf der Drehachse ein Drehmoment. Da sich das System im Gleichgewicht befindet (das Thema Gleichgewicht wird außerdem in folgenden Statik-Skripten ausführlich behandelt) müssen sich die Drehmomente auf der Drehachse gegenseitig aufheben. Falls dies nicht der Fall wäre würde sich der Stab um die Drehachse drehen.
Wichtige Regeln für Momente, die in dieser Übungsaufgabe angewendet werden müssen, sind die Vorzeichenregel für Momente und die Regel, das Momente addiert und subtrahiert werden können.
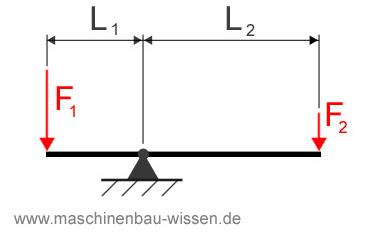
Übungsaufgabe – Moment & Gleichgewicht
Es ergibt sich die Formel:
M = F1*L1 - F2*L2
Da wir wissen, dass sich das System im Gleichgewicht befindet, muss das Gesamte Moment auf der Drehachse gleich 0 sein. Damit ergibt sich die Formel wie folgt:
0 = F1*L1 - F2*L2 => F1*L1 = F2*L2 => F1 = F2*L2/L1
Folgende Werte werden vorgegeben:
L1 = 1m
L2 = 3m
F2 = 10N
Daraus folgt:
F1 = 10N * 3m/1m = 30N
Man erkennt, dass bei den Bedingungen dieses Beispiels aus einem längeren Hebelarm eine kleinere Kraft folgt. Ist der gegenüberliegende Hebelarm wie in diesem Beispiel dreimal so lang, muss die angreifende Kraft nur noch 1/3 von der entgegengesetzt drehenden Kraft betragen.
Beispiel 2 – geknickter Stab
In diesem Beispiel soll die Bestimmung des Hebelarms veranschaulicht werden. Dazu werden zwei Szenarien verglichen. Die beiden Systeme sind im Bild unten nebeneinander dargestellt.
Auf den ersten Blick sehen die beiden Aufgaben fast gleich aus. Beide Stäbe haben die gleiche Form und die gleiche Länge. Was unterschiedlich ist, ist die Richtung der angreifenden Kraft F, die ein Moment M auslöst.
Wie im vorhergehenden Statik-Skript über Drehmomente bereits erwähnt wurde, ist der Hebelarm immer senkrecht zum Kraftvektor. Somit ergeben sie die beiden unterschiedlichen Hebelarme - L1 und L2 - wie sie im Bild unten zu sehen sind.
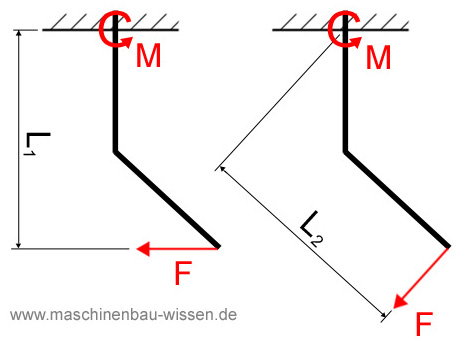
Beispiel-Aufgabe – Drehmoment & Hebelarm
Wenn man Statik-Aufgaben* löst, die mit Momenten zu tun haben, ist es also wichtig, dass man sich nicht von der Form des Stabes verwirren oder täuschen lässt. Der Hebelarm ist immer senkrecht zu Kraftvektor (bzw. zur Wirkungslinie der Kraft) und entspricht der kürzesten Strecke zur Drehachse.
Weitere Beispiel-Aufgaben für Momente
Im Folgenden sind drei weitere Beispiel-Aufgaben dargestellt, die zeigen wie man den richtigen Hebelarm ermittelt.
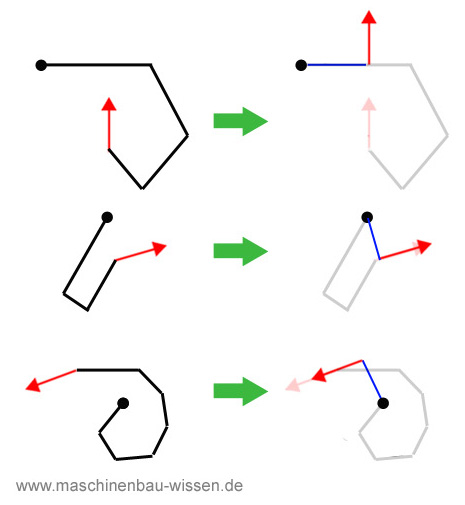
Beispiel-Aufgaben – Drehmoment & Hebelarm
Man denke hier auch an die Regel, dass Kräfte entlang ihrer Wirkungslinie verschoben werden dürfen.
Links abgebildet ist immer der Stab, Drehachse und angreifende Kraft. Rechts ist in blau der anzuwendende Hebelarm dargestellt.



