In diesem Mechanik-Skript wird gezeigt, wie man die Belastung auf Biegung berechnen kann. Genauer gesagt geht es hier um die Berechnung der Biegespannung eines Balkens, der mit einer Querkraft belastet wird (unterscheiden Sie hierzu die reine bzw. querkraftfreie Biegung). Zum Verständnis der Biegebelastung eines Balkens folgen hier einige wichtige Grundlagen:

Grundlagen der Biegebelastung

Sofern lange, dünne Bauteile wie etwa Wellen, Stäbe oder Balken quer zur Bauteilachse mit einem Biegemoment belastet werden, entstehen sowohl Zug- als auch Druckspannungen, aus denen letztendlich eine Durchbiegung resultiert. Wenn man diese Biegung berechnen möchte, ist folgendes Verständnis wichtig:

Im Bereich der Zugkräfte wird das betroffene Bauteil gedehnt, wogegen es in dem Bereich, in dem die Druckkräfte wirken, gestaucht wird. Die mittig zwischen diesen beiden Bereichen liegende Schicht ist die sogenannte neutrale Faser. Entlang dieser Linie findet weder eine Dehnung noch eine Stauchung statt. Laut Definition nimmt die von der neutralen Faser ausgehende Spannung in Richtung der äußeren Bauteilkante stetig immer weiter zu. Daraus resultiert, dass am äußeren Bauteilrand die stärksten Spannungen auftreten.

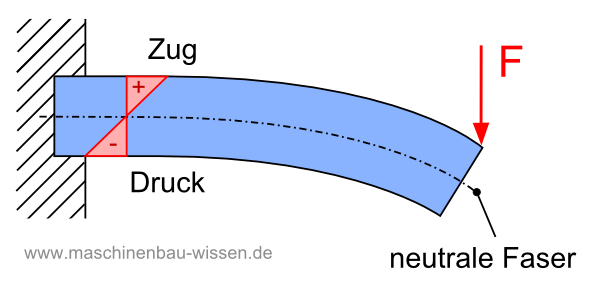
Abbildung: Biegebelastung eines Balkens mit Zug- und Druckspannungen

Mehr zum Thema Balkenbiegung finden Sie in der Hauptrubrik:
Balkenbiegung Skript

Beispiel 1 - Beanspruchung eines Bauteils auf Biegung

Der Stab, die Welle oder der Balken wird infolge der Kraft F auf Biegung beansprucht, wobei sich die ursprünglich gerade Stabachse durchbiegt. Wie ersichtlich, entstehen innerhalb des Querschnitts sowohl Zug- als auch Druckspannungen. Um diesen Sachverhalt anschaulich zu verdeutlichen, wurde der Umfang der Durchbiegung in der Skizze stark übertrieben dargestellt.

Hier noch der Hinweis, dass es sich in diesem Beispiel um eine sogenannte gerade Biegung und eine Querkraftbiegung handelt. Mehr über die unterschiedlichen Arten der Biegung lesen Sie in diesem Skript:

Arten der Biegung

Abbildung: Biegebelastung eines Balkens mit Zug- und Druckspannungen

Die neutrale Faser (Strich-Punkt-Darstellung) ist vollkommen spannungslos, während an den Rändern des Stabes die stärksten Spannungen erkennbar sind. Für symmetrische Querschnitte gilt: Die Zug- und Druckspannungen verteilen sich stets linear, d. h. gleichmäßig über den gesamten Bauteilquerschnitt.

Biegespannung berechnen - Formel

Zur Berechnung der Biegespannung wird folgende Formel verwendet:

σ_b – Biegespannung
M_b – Biegemoment
W – Widerstandsmoment

Aus dieser Formel wird ersichtlich, dass die Biegespannung σ_b abhängig ist

• vom Biegemoment M_b und
• vom Widerstandsmoment W.

Wie man diese beiden Größen berechnen kann, lesen Sie im Folgenden.

Das Biegemoment M_b berechnen

 Nachfolgend wurden ausschließlich Formeln für einfache Belastungsfälle angeführt. Um unübersichtliche und komplizierte Berechnungen zu vermeiden, erfolgt die Ermittlung des Biegemoments für alle anderen Fälle mittels Formeln und Tabellen, die in Tabellenbüchern zu finden sind.

In der Praxis finden sich folgende Belastungsfälle für Biegemomente M_b bei einwirkender Einzelkraft besonders häufig:

• einseitig eingespannter Träger
• Träger, der auf zwei Stützen ruht

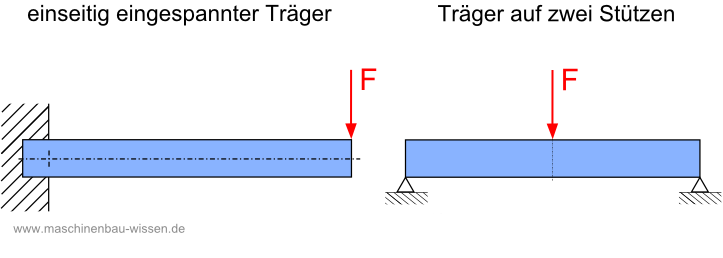
Zwei typische Belastungsfälle für Balkenbiegung mittels Querkraft

Für den einseitig eingespannten Träger, wie er im Beispiel 1 vorliegt, gilt:

M_b – Biegemoment
F – Kraft (Querkraft)
x – Abstand (der Kraft F vom Festlager des Balkens)

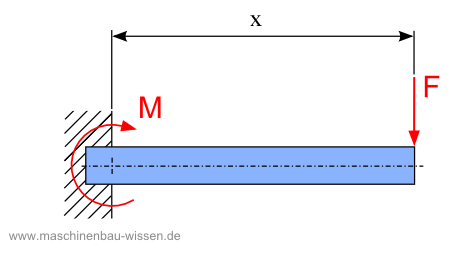
Biegemoment an einem einseitig eingespannten Balken

Hier sind einige Links, in denen Sie mehr über die Grundlagen der Berechnung des Biegemoments lesen können:

• Moment, Drehmoment, Biegemoment - Grundlagen
• Moment - Beispiele
• Momentengleichgewicht – Beispiel
• Schnittreaktionen, Kräfte- & Momentengleichgewicht
• Schnittreaktionen, Kräfte- & Momentengleichgewicht - Aufgabe

Das axiale Widerstandsmoment W

Das axiale Widerstandsmoment ist ein Maß für den Widerstand gegen Durchbiegung. Deshalb wird es oft auch als Biegewiderstandsmoment bezeichnet. Für die Größe des Widerstandsmomentes ist allein die Geometrie der jeweils betrachteten Bauteil-Querschnittsfläche ausschlaggebend.

Zur Berechnung des Widerstandsmomentes ist die Definition der exakten Lage der neutralen Faser innerhalb des Querschnittes Grundvoraussetzung. Die neutrale Faser verläuft exakt durch den Schwerpunkt des Querschnitts. Ausgehend von dieser Linie lässt sich dann der größtmöglichen Abstand zur Außenkante (Randfaser) ermitteln, Dort sind die höchsten Bauteilbelastungen bzw. die größten Spannungen zu erwarten.

Das Widerstandsmoment errechnet sich als Quotient aus dem Flächenträgheitsmoment und dem Abstand (a_max), der das Maß von der spannungsfreien neutralen Faser bis zur Außenkante (Randfaser) darstellt.

W – axiales Widerstandsmoment
I – axiales Flächenmoment 2. Grades (auch Flächenträgheitsmoment)
a_max: größter Abstand der Randfaser zur neutralen Faser

Weiterführende Informationen über das Widerstandsmoment finden Sie in folgenden Beiträgen:

• Grundlagen Widerstandsmoment
• Widerstandsmoment & Flächenträgheitsmoment einfacher Querschnitte berechnen
• Widerstandsmoment & Flächenträgheitsmoment eines Kreisquerschnitts berechnen
• Widerstandsmoment & Flächenträgheitsmoment beliebiger Querschnitte berechnen

Das Flächenträgheitsmoment

Das Flächenträgheitsmoment (auch Flächenmoment 2. Grades) – genauer gesagt das axiale Flächenträgheitsmoment - definiert den Widerstand eines Bauteiles gegenüber Biegung. Die Berechnung erfolgt als Ableitung aus der Querschnittgeometrie des Stabes, Balkens, der Welle o. ä. Die Angabe des Flächenträgheitsmomentes erfolgt üblicherweise in der SI-Einheit m4.
Zur Berechnung des Flächenträgheitsmomentes nutzt man am besten passende Tabellen, da die eigenständige Herleitung relativ aufwändig ist.

Im Bild unten sehen Sie zwei Beispiele für die Berechnung des Flächenträgheitsmoments und des Biegewiderstandsmoments.

Mit den berechneten Größen – Biegemoment, Flächenträgheitsmoment und Widerstandsmoment – kann man nun zur zu Beginn dargestellten Formel gehen und die Biegespannung berechnen.

Weitere Skripte mit den Grundlagen des Flächenträgheitsmoments finden Sie hier:

• Grundlagen - Flächenträgheitsmoment 
• Widerstandsmoment & Flächenträgheitsmoment einfacher Querschnitte berechnen
• Widerstandsmoment & Flächenträgheitsmoment eines Kreisquerschnitts berechnen
• Widerstandsmoment & Flächenträgheitsmoment beliebiger Querschnitte berechnen

Beispiel 2 - Träger ruht auf zwei Stützen

Das zweite Beispiel zeigt den zweiten typischen Fall für eine Biegebelastung. Hier kann man die Biegung relativ ähnlich berechnen.

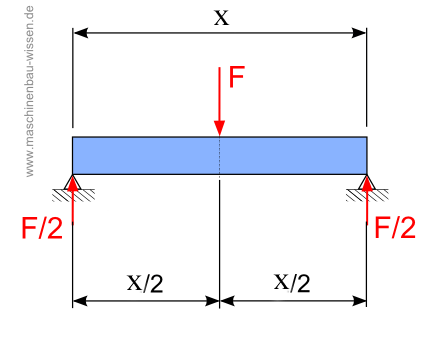
Balken mit mittiger Querkraft belastet

Auf den auf zwei Stützen ruhenden Träger wirkt mittig die Kraft F. Das Biegemoment ergibt sich, indem der Biegequerschnitt, wie im Bild dargestellt, von der Seite betrachtet wird. Es lassen sich sowohl die Kraft F/2 als auch der Abstand x/2 erkennen. Das Biegemoment berechnet sich nun wie folgt:

M_b – Biegemoment
F – Kraft (Querkraft)
x – Abstand (der Kraft F vom Festlager des Balkens)

Das Widerstandsmoment und Flächenträgheitsmoment sind vom Biegemoment unabhängig und lassen sich genauso berechnen wie im vorhergehenden Beispiel. Mit dem Biegemoment kann dann auch die Biegespannung ermittelt werden.

Anmerkung:
Bei den hier berechneten Biegespannungen und Biegemomenten handelt es sich um die jeweils auftretenden Maximal-Werte.

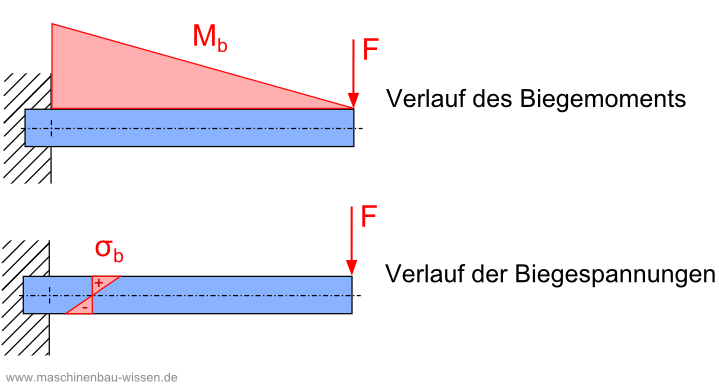
Unterschiedliche Werte für Biegemoment und Biegespannung

Die Höhe des Biegemoments ist allgemein betrachtet abhängig vom Messpunkt am Balken (i.d.R. als x-Koordinate deklariert).
Die Höhe der Biegespannung ist abhängig von der Höhe des Biegemoments und somit wiederum abhängig vom Messpunkt am Balken. Betrachtet man das Innere des Balkens, ist die Biegespannung in der Randfaser mit dem größten Abstand zur neutralen Faser am höchsten. Die Biegespannung ist also auch abhängig von der Stelle innerhalb des Balkenquerschnitts, an der gemessen wird (i.d.R. die z-Koordinate).