Wie bereits in einem hervorgehenden Statik-Skript angekündigt, werden wir nun näher auf die Schnittreaktionen - also die inneren Kräfte - eingehen.
Die inneren Kräfte sind Kräfte, die im Inneren eines Bauteils entstehen, wenn diese durch äußere Kräfte und Momente belastet wird. Die inneren Kräfte eines Balkens werden durch Freischneiden an der Stelle x freigelegt wie im Bild unten zu sehen ist. Das Thema Freischneiden und Schnitt wurde in diesem Statik-Skript beschrieben: Freischneiden

Schnittreaktionen Balken
Bei einem Schnitt entstehen zwei Schnittufer und damit zwei getrennt voneinander zu betrachtende statische Systeme. Die entstandenen statischen Systeme liegen – jedes für sich – im Gleichgewicht. Genauer gesagt bedeutet dies, dass die inneren und äußeren Kräfte im Gleichgewicht zueinander liegen. Es gilt zu beachten, dass alle Schnittkräfte auf der linken Seite des Schnitts positiv sind, alle Schnittkräfte auf der rechten Seite des Schnitts negativ.
Es gibt folgende innere Kräfte bzw. Schnittreaktionen:
N = Normalkraft:
Die Normalkraft verläuft in Richtung der Balkenachse. Es handelt sich dabei um eine Zugkraft oder eine Druckkraft.
Q = Querkraft:
Die Querkraft verläuft senkrecht zur Normalkraft. Hierbei handelt es sich um eine Schubkraft.
M = Biegemoment:
Das Biegemoment verläuft um den Schwerpunkt der Schnittfläche.
Alle Schnittreaktionen sind abhängig von der Koordinate x:
Es folgt: N(x), Q(x), Mb(x)
Gleichgewichtsbedingungen beim Freischneiden
Bezüglich der Gleichgewichtsbedingungen gilt:
Die Summe aller Normalkräfte und aller äußeren Kräfte in x-Richtung ist gleich 0.
=> Links vom Schnitt: +N(x) + ∑Fx = 0 => N(x) = - ∑Fx
=> Rechts vom Schnitt: -N(x) + ∑Fx = 0 => N(x) = + ∑Fx
Die Summe aller Querkräfte und aller äußeren Kräfte in y-Richtung ist gleich 0.
=> Links vom Schnitt: +Q(y) + ∑Fy = 0 => Q(y) = - ∑Fy
=> Rechts vom Schnitt: -Q(y) + ∑Fy = 0 => Q(y) = + ∑Fy
Die Summe aller Biegemomente und aller äußeren Momente ist gleich 0.
=> Links vom Schnitt: +Mb(x) + ∑M = 0 => Mb(x) = - ∑M
=> Rechts vom Schnitt: -Mb(x) + ∑M = 0 => Mb(x) = + ∑M
Dabei gilt:
N(x), Q(x), Mb(x) = innere Kräfte und Momente
Fx, Fy, M = äußere Kräfte und Momente
Die Schnittreaktionen N(x), Q(x) und Mb(x) sind an beiden Schnittufern (links sowie rechts) identisch, daher erfolgt die Berechnung in der Regel nur auf einer Seite.
Vorzeichenregel für Biegemoment
Für Biegemomente gelten folgende Vorzeichenregeln:
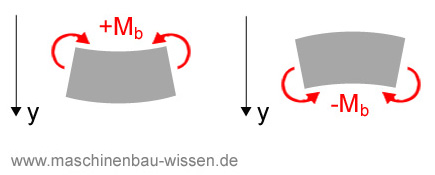
Vorzeichenregeln Biegemoment
- Liegt eine Durchbiegung in y-Richtung vor, handelt es sich um ein positives Biegemoment.
- Liegt eine Durchbiegung entgegen der y-Richtung vor, handelt es sich um ein negatives Biegemoment (siehe hierzu die Abbildung oben).



