Werkstofftechnik - Metall
In diesem Bereich finden Sie Skripte zum Thema Kinetik.
Die Kinetik ist ein Teilgebiet der Mechanik und befasst sich mit der Bewegung von Punkten und Körpern im Raum unter Einfluss von Kräften. Zusammen mit der Statik gehört die Kinetik zum Gebiet der Dynamik. Im Gegensatz zur Kinetik beschäftigt sich die Statik mit dem Kräftegleichgewicht von Körpern, die nicht beschleunigt oder bewegt werden.
Der italienische Naturwissenschaftler Galileo Galilei formulierte die Goldene Regel der Mechanik* vor rund 400 Jahren folgendermaßen:
„Was man an Kraft spart, muss man an Weg zusetzen.“
Die Goldene Regel der Mechanik* besitzt für alle kraftumformenden Einrichtungen Gültigkeit. Sie kann als Gleichung oder Proportionalität formuliert werden, wobei heute auch alle physikalischen Gültigkeitsbedingungen bekannt sind.
Sofern man die Reibung vernachlässigt, gilt für alle kraftumformenden Systeme die Formel:
Die Goldene Regel der Mechanik anschaulich erklärt
Wenn man einen Gegenstand am Boden verschiebt oder ihn vom Boden nach oben hebt, wird physikalische Arbeit verrichtet. Für beide Situationen gilt, dass eine bestimmte Kraft in Richtung Strecke, also längs, überwunden werden muss.
Die Goldene Regel der Mechanik sagt aus, dass sich Arbeit vergrößert, wenn die längs zur Wegstrecke wirkende Kraft, die dabei überwunden werden muss, größer wird. Die Arbeit wird jedoch auch dann größer, wenn sich der Weg, der zurückzulegen ist, bei gleichem Widerstand verlängert. Deshalb errechnet sich physikalische Arbeit aus der Kraftkomponente multipliziert mit der Wegstrecke.
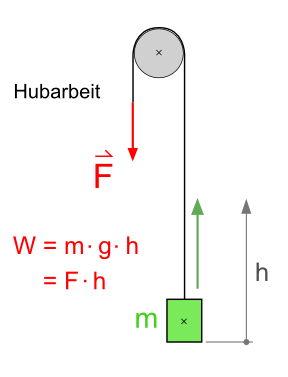
Zusammenhang zwischen Kraft, Weg und Arbeit am Beispiel der Hubarbeit
Die Variable W (abgeleitet von "work") bedeutet Arbeit. Sie wird in Newtonmeter (Nm) oder Joule (J) angegeben. Die Kraftkomponente Fs wirkt in Wegrichtung und trägt die Einheit Newton (N). Der zurückgelegte Weg s wird in Meter (m) angegeben.
Merke: Arbeit von 1 Joule wird verrichtet, wenn ein Körper mit einer Gewichtskraft von 1 Newton 1 Meter angehoben wird.
Beispiele - Goldene Regel der Mechanik
Beispiel 1: Schiefe Ebene
Anstatt einen Gegenstand mit seiner absoluten Gewichtskraft vom Boden anzuheben, kann er den gleichen Höhenunterschied entlang einer schiefen Ebene zurücklegen. Der zurückgelegte Weg wird länger. Dafür ist weniger Kraft notwendig um den gewünschten Höhenunterschied zu erzielen.
Man kann zum Beispiel eine Masse mit Hilfe einer Rampe auf eine höhere Position bringen. Die Rampe stellt aus Sicht der Kinetik eine schiefe Ebene dar. Wenn die Masse auf der Rampe nach oben geschoben wird, wird Hubarbeit verrichtet. Die Formel für Hubarbeit lautet wie folgt:
Die Masse wird zur Erreichung der gewünschten Höhe über einen bestimmten Weg geschoben, der umso kürzer ist, je steiler die Steigung der Ebene ist. Die erforderliche Kraft steigt jedoch auch mit einer höheren Steigung.
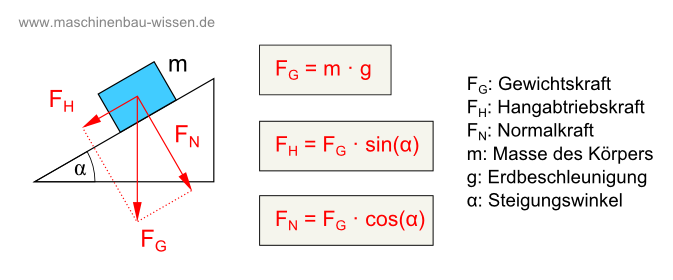
Berechnung einer Masse auf der schiefen Ebene
Im Umkehrschluss heißt dies jedoch auch, dass man die erforderliche Kraft reduzieren kann, indem man den Steigungswinkel verringert und somit den Schiebeweg erhöht. Die Arbeit bleibt (unter Vernachlässigung der Reibung) wiederrum gleich.
Beispiel 2: Flaschenzug
Der Körper wird bei einem Flaschenzug mithilfe einer Rollen-Seil-Konstruktion nach oben gehoben. Für das Ziehen des Seiles ist eine kleinere Kraft als die Gewichtskraft erforderlich. Allerdings muss länger am Seil gezogen werden, als beim Hochziehen auf direktem Weg.
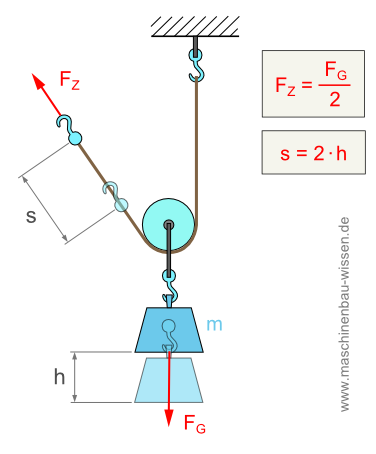
Flaschenzug mit Zugrichtung nach oben
Anhand dieser beiden Beispiele für die Goldene Regel der Mechanik, sollte dieser alte Grundsatz gut verständlich geworden sein. Die Kenntnis über die beschriebenen Zusammenhänge trägt auch zum Verständnis für viele weitere Grundlagenthemen der Mechanik und Kinetik* bei.
Der Bewegungszustand eines physikalischen Körpers (z. B. Auto, Ball, Rakete, Elektron), lässt sich über die physikalische Größe Geschwindigkeit definieren. Sobald eine Änderung dieses Bewegungszustandes erfolgen soll, muss eine bestimmte Kraft aufgewendet werden, wobei die Größe dieser Kraft von der Masse des physikalischen Körpers abhängt.
Das bedeutet, dass der Bewegungszustand des Körpers sowohl von seiner Masse als auch von seiner Geschwindigkeit abhängig ist. Die Beschreibung dieses Faktums erfolgt mithilfe der physikalischen Größe Impuls. Diese Größe, die manchmal auch als Bewegungsgröße bezeichnet wird, lässt sich berechnen.
Berechnung des Impulses
Der Impuls ist eine vektorielle Größe. Seine Richtung stimmt mit der Bewegungsrichtung des Körpers überein. Weil das internationale Einheitensystem keine eigene Maßeinheit vorsieht, verwendet man zur Berechnung: ein Kilogramm mal Meter durch Sekunde (kg*m/s).
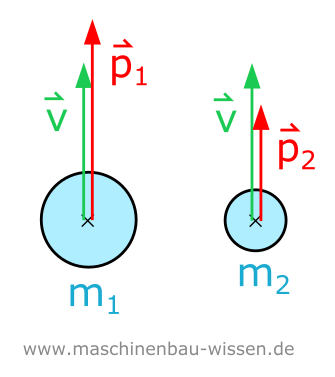
Impuls auf unterschiedliche Massen
Der Impuls errechnet sich demnach aus der Masse mal Geschwindigkeit:
Darüber hinaus lässt sich zwischen Masse, Impuls sowie der kinetischen Energie folgender Zusammenhang herleiten und berechnen:
Damit sich die Geschwindigkeit des Körpers ändert, ist die Impulsübertragung erforderlich, wobei man bei der Berechnung davon ausgeht, dass der Impuls, der pro Zeiteinheit übertragen wird, der Kraft F entspricht. Zur Berechnung dient die Formel:
Die Besonderheit des Impulses besteht darin, dass er eine Erhaltungsgröße ist. Das heißt, dass jeder bewegliche physikalische Körper kann seine Impulse, teilweise oder ganz, auf andere Körper übertragen oder anderen Körpern übernehmen. Sobald ein Körper auf einen anderen trifft, ergibt das einen Stoß, bei dem der Gesamtimpuls erhalten bleibt, obwohl sich die einzelnen Impulse ändern.
Wie für die Energie gilt auch für den Impuls ein Erhaltungsgesetz, das die Bezeichnung "Gesetz von der Erhaltung des Impulses" oder kurz, Impulserhaltungssatz trägt.
Der Impulserhaltungssatz lautet: In einem physikalisch abgeschlossenen System, ohne äußere Krafteinwirkung oder anderen Wechselwirkungen mit der Umgebung, bleibt der Gesamtimpuls stets erhalten. Hingegen können Kräfte im Innern des Systems in beliebiger Art und Weise wirken.
Der Impulserhaltungssatz ist ein grundsätzlicher Erfahrungssatz, der eine der wichtigsten physikalischen Gesetzmäßigkeiten beschreibt. Er gilt sowohl in der Makro- als auch in der Mikrophysik. Unabhängig von der Energie findet demnach das Gesetz von der Impulserhaltung sowohl in der klassischen Physik als auch in der Quantenmechanik sowie in der Relativitätstheorie Anwendung, indem es beispielsweise Stoßprozesse eindeutig beschreibt. Unabhängig davon, ob es sich um einen elastischen oder einen unelastischen Stoß handelt, besagt der Impulserhaltungssatz, dass der Gesamtimpuls aller beteiligten Stoßpartner vor und nach dem Stoß identisch ist.
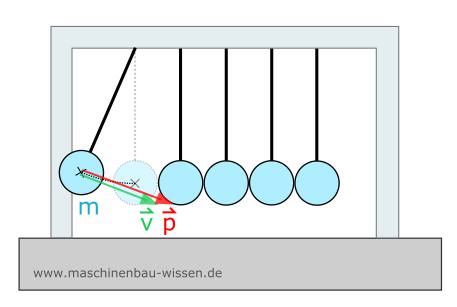
Impulserhaltung bei einem Pendel
Die Impulserhaltung in der Newtonschen Mechanik
Der Impulserhaltungssatz leitet sich unmittelbar aus dem zweiten und dritten Newtonschen Gesetz ab.
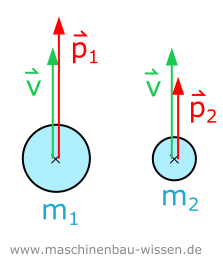
Impuls zweier unterschiedlicher Massen
Gemäß dem zweiten Newtonschen Gesetz ist die Impulsänderung innerhalb einer bestimmten Zeit mit der, auf den Körper von außen einwirkenden Kraft, identisch. Es gilt:
Sofern von außen keine Kräfte wirken, findet das dritte Newtonsche Gesetz Anwendung. Es besagt, dass es für jede Kraft eine gleichgroße Gegenkraft gibt, die entgegengesetzt wirkt. Daher ist die Vektorsumme der beiden Kräfte null. Weil diese Gesetzmäßigkeit für alle Kräfte innerhalb eines geschlossenen physikalischen Systems gilt, ist auch die Vektorsumme aller Kräfte, innerhalb des Systems gleich null. Folglich verändert sich die Größe des Gesamtimpulses nicht. Es gilt:
Laut Impulserhaltungssatz wird p somit zu einer Konstanten. Für den Fall, dass der Impuls lediglich von der Geschwindigkeit abhängt, bewegt sich der Masseschwerpunkt des physikalischen Systems mit konstanter Geschwindigkeit.
In der Natur, im Alltag und in der Technik treten vielfältige Arten von Stößen auf. Hierbei kann die Einteilung bezüglich der Energiebilanz (elastisch, unelastisch), nach der Lage der Körper während des Stoßes (gerade, schief) und danach, ob der Stoß zentral oder nicht zentral auftritt, erfolgen. Bei der theoretischen Betrachtung und Berechnung von Stößen handelt es sich in aller Regel um Idealisierungen, die in der Praxis nur annähernd vorkommen.
Elastische, teilelastische und unelastische und Stöße
Üblicherweise wird bei dieser Art der Einteilung ausschließlich die kinetische Energie der Stoßpartner betrachtet. Das bedeutet, dass sie sich in einer Ebene bewegen und dass keine Rotation auftritt.
Elastischer Stoß:
Diese Stoßart wird häufig auch als idealer Stoß bezeichnet. Sie liegt vor, wenn die kinetische Energie der Stoßpartner vor und nach dem Zusammenstoß gleich groß ist, wobei lediglich elastische Verformungen auftreten.
Unelastischer Stoß:
Hier bewegen sich die Körper nach dem Zusammenstoß entweder ungebremst mit einer gemeinsamen Geschwindigkeit weiter, wobei ausschließlich unelastische Verformungen auftreten. Die andere Möglichkeit besteht darin, dass während des Stoßes die kinetische Energie in eine andere Energieform umgewandelt wird. Das wäre beispielsweise der Fall, wenn ein verformbarer Gegenstand gegen eine feste Wand geworfen wird.
Realer Stoß / Teilplastischer Stoß / Teilelastischer Stoß:
Der reale Stoß wird oft auch als teilelastischer bzw. teilplastischer Stoß bezeichnet, da die Verformung der Körper teileweise plastisch aber teilweise elastisch ist. Hier ist die Wechselwirkung zwischen den Stoßpartnern teils elastisch, teils unelastisch. Es erfolgt die Umwandlung eines Teils der kinetischen Energie der Stoßpartner in eine andere Energieform. Dieser Fall tritt in der Praxis am häufigsten auf.
Gerade und schiefe Stöße
Hier werden die Arten der Stöße nach der Lage, in der sich die Körper vor dem Zusammenstoß befinden, unterschieden. Bei geraden Stößen liegen sowohl die Geschwindigkeiten als auch die Richtungen aller Stoßpartner auf einer Linie. Diese verläuft durch den jeweiligen Schwerpunkt aller beteiligten Körper. Schiefe Stöße liegen vor, wenn sich die Parameter nicht auf einer gemeinsamen Linie befinden.
Zentrale und nicht zentrale Stöße
Hier erfolgt die Einteilung nach der Lage der am Stoß beteiligten Körper. Bei zentralen Stößen steht die Verbindungsgerade aller Körperschwerpunkte senkrecht auf der Berührungsfläche, die die Stoßpartner beim Zusammenstoß ausbilden. Ein Beispiel hierfür ist der Zusammenstoß zweier Kugeln. Sobald diese Bedingung nicht erfüllt ist, liegt ein nicht zentraler Stoß (auch exzentrischer Stoß genannt) vor.
Ein unelastischer Stoß weist folgende Merkmale auf:
- Die Schwerpunkte der Stoßkörper liegen auf einer geraden Linie. Diese Verbindungsgerade steht senkrecht auf der Berührungsfläche, die sich beim Zusammenstoß der Körper ausbildet.
- Durch den Stoß entstehen keine elastischen Wechselwirkungen.
- Nach dem Stoß bewegen sich die Körper mit einer gemeinsamen Geschwindigkeit weiter
- Ein Teil oder die gesamte kinetische Energie wird in innere Energie (U) umgewandelt, die sich berechnen lässt.
Beispiele für unelastische Stöße sind der Zusammenstoß zweier Autos oder der Hammerschlag auf einen Nagelkopf. Ein unelastischer Stoß kann auch bei Atomen und Elementarteilchen auftreten.
Bei der Betrachtung von Ergebnissen, die sich aus der Berechnung unelastischer Stöße ergeben, ist zu beachten, dass es sich um Idealisierungen handelt, die in der Praxis nur annähernd auftreten. So wird beim ideal unelastischen Stoß der gesamte Anteil der kinetischen Energie in innere Energie umgewandelt. Nach dem Stoß „kleben“ die beiden Massen aneinander und bewegen sich gemeinsam mit derselben Geschwindigkeit v´2 fort.
Unelastischer Stoß - Berechnung
Bei vielen Anordnungen (z. B. Auffahrunfall), lässt sich ein elastischer Stoß mittels Impulserhaltungssatz berechnen. Hier ist es allerdings wichtig, die gesamte Anordnung als geschlossenes System, ohne Reibungseffekte zu betrachten.
Es gelten die beiden Erhaltungssätze:
Ekin – kinetische Energie (vor dem Stoß) [J]
E´kin – kinetische Energie nach dem Stoß [J]
U – innere Energie [J]
p – Impuls vor dem Stoß
p´ – Impuls nach dem Stoß
Kinetische Energie und Impuls vor dem Stoß:
Ekin – kinetische Energie (vor dem Stoß) [J]
m1 – Masse 1
m2 – Masse 2
v1 – Geschwindigkeit von Masse 1 (vor dem Stoß)
v2 – Geschwindigkeit von Masse 2 (vor dem Stoß)
p – Impuls vor dem Stoß
Kinetische Energie und Impuls nach dem Stoß:
E´kin – kinetische Energie nach dem Stoß [J]
m1 – Masse 1
m2 – Masse 2
v´2 – Geschwindigkeit von Masse 2 nach dem Stoß
p´ – Impuls nach dem Stoß
Berechnung der Geschwindigkeit v´2 nach dem unelastischen Stoß
Die Geschwindigkeit v´2, die nach dem unelastischen Stoß vorliegt, lässt sich wie folgt berechnen:
m1 – Masse 1
m2 – Masse 2
v1 – Geschwindigkeit von Masse 1 (vor dem Stoß)
v2 – Geschwindigkeit von Masse 2 (vor dem Stoß)
v´2 – Geschwindigkeit von Masse 2 nach dem Stoß
Fährt hingegen ein Pkw gegen einen Baum, wird die gesamte kinetische Energie in andere Energieformen, wie Deformation und Reibung umgewandelt, wobei die Höhe des Verlustes an kinetischer Energie das Maß der Zerstörung bestimmt. Hier gilt zur Berechnung der Energieerhaltungssatz der Kinetik.
Die innere Energie U lässt sich aus dem Energieerhaltungssatz berechnen:
Ekin – kinetische Energie (vor dem Stoß) [J]
E´kin – kinetische Energie nach dem Stoß [J]
U – innere Energie [J]
m1 – Masse 1
m2 – Masse 2
v1 – Geschwindigkeit von Masse 1 (vor dem Stoß)
v2 – Geschwindigkeit von Masse 2 (vor dem Stoß)



