In diesem Artikel soll der Begriff "Spannung" innerhalb des Gebiets Technische Mechanik und Festigkeitslehre erläutert werden (also nicht Spannung in Verbindung mit Strom/Elektrik).
Geht es im Hinblick auf Festigkeitsfragen um die Bewertung von wirkenden Kräften auf Bauteile, ist nicht die in einem Querschnitt eines Bauteils wirkende Kraft entscheidend, sondern die Kraft pro Einheitsfläche. Das ist der Kraftanteil, der auf ein Flächenelement des Bauteilquerschnittes wirkt. Bezieht sich die Kraftgröße auf eine Flächeneinheit, wird von Spannung gesprochen, die wie folgt definiert wird:

bzw.

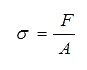
SI-Einheit: [N/m²]

Hier liegt ein entscheidender Unterschied zwischen der Festigkeitslehre und der Statik wie wir sie bisher kennengelernt haben. Die Festigkeitslehre erweitert die Betrachtung um die dritte Dimension, wodurch die Betrachtung von Spannungen möglich wird.

Die Einheit der Spannung wird in N/m² angegeben, die auch als 1 Pa (Pascal) bezeichnet wird. In der Technik relevante Spannungswerte liegen jedoch deutlich über 1 Pa. Deshalb werden sie in der Regel in Megapascal (1 Mpa = 10⁶ Pa) oder auch in Gigapascal (1 Gpa = 10⁹ Pa) angegeben, um der Kraft technischer Spannung gerecht zu werden. In der deutschen Technik-Literatur findet auch bevorzugt die Einheit 1N/mm² = 1MPa Verwendung.

Spannungsarten in Abhängigkeit von der Kraftrichtung

Doch nicht nur die Größe der Kraft ist für die Charakterisierung von Spannung maßgebend, auch die Richtung, aus der die Kraft auf die Flächeneinheit einwirkt, muss Berücksichtigung finden.

Es wird deutlich, bei der Betrachtung der Spannung in der technischen Mechanik* zwischen zwei verschiedenen Fällen unterschieden werden muss:

a) Senkrechte Krafteinwirkung auf die Schnittfläche

In diesem Falle wirkt die Normalkraft F, die sowohl als Druck- als auch als Zugkraft wirken kann. Bei der Berechnung der dazugehörigen Spannung, entsprechend der oben genannten Gleichung, wird (in Anlehnung an die Normalkraft) konsequenterweise die Normalspannung ( = σ) ermittelt. Je nach Richtung, aus der die Normalkraft auf die Flächeneinheit einwirkt, wird zwischen einer Druckspannung (gekennzeichnet durch ein negatives Vorzeichen) und einer Zugspannung (gekennzeichnet durch ein positives Vorzeichen) unterschieden. In Schriftform sieht das so aus:

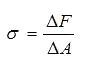
b) Parallele Krafteinwirkung zur Schnittfläche

Wirkt eine Kraft parallel zur Schnittfläche, handelt es sich um eine Querkraftbelastung, aus der wiederum eine Schubspannung resultiert. Diese Spannung wird mit dem Symbol τ gekennzeichnet. Dadurch entsteht folgende Formel:

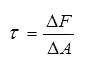
Allgemein betrachtet kann gesagt werden, dass beide Spannungsarten gemeinsam auftreten und sogar über dem Balkenquerschnitt von Punkt zu Punkt unterschiedlich ausfallen können. Die Normalspannung, die durch das Aufprägen eines reinen Biegemomentes M im Balken resultiert, wird sich von einer Zugspannung auf der unteren Balkenseite linienförmig über den Querschnitt des Balkens in eine Druckspannung auf der oberen Balkenseite verwandeln.