In dieser Beispiel-Aufgabe wollen wir die Verformung in einem Stab berechnen, der unter Druckkraft steht. Um die Aufgabe* verstehen und lösen zu können, ist ein wenig Grundwissen im Bereich Technische Mechanik und Festigkeitslehre erforderlich.
Aufgabe - Die Verformung in einem Stab berechnen
Gegeben sind die Geometrie und die Kraft, die als Druckkraft auf den Stab wirkt. Mit diesen beiden Größen ist die Berechnung der Verformung realisierbar. Das Vorgehen ist das gleich, wie bei der Berechnung der Verformung unter einer Zugkraft, mit dem einzigen Unterschied, dass in der Mechanik der Druck ein negatives Vorzeichen erhält.
Zudem ist die Art der Verformung bei einer Zugbelastung eine Dehnung, während wir unter einer Druckbelastung einer Stauchung vorfinden. Was wir in diesem Beispiel auch betrachten wollen, ist die Querkontraktion berechnen – also die Verformung in Querrichtung (90° zur Belastungsrichtung).
Gegeben sind:
a) Die Belastung:
Druckkraft: F = -4728 N
Die Kraft wirkt von oben im 90°-Winkel auf den Stab ein. Der Stab steht gerade auf einem festen Untergrund.
b) Die Geometrie:
Länge = 27 mm
Durchmesser = Ø6 mm
Querschnittsform: rund / kreisförmig
Verformung Grundwissen
Bei der Verformung eines Stabe unter Zug- oder Druckbelastung kommt es in erster Linie zu einer Längenänderung in der Belastungsrichtung. Das heißt, der Stab wir unter einer Zugkraft gedehnt (Dehnung) bzw. unter einer Druckkraft gestaucht (Stauchung). Dies ist die Verformung in Längsrichtung.
Gleichzeitig kommt es jedoch auch zu einer Formänderung in der Querrichtung. Es handelt sich hier um eine i.d.R. geringere Verformung, als der in Längsrichtung (da ein Stab meistens deutlich länger ist als breit).
Bei dieser Querkontraktion kommt es zu einer Änderung des Durchmessers. Logischer Weise wird ein Stab unter Zuglast dünner und unter Drucklast dicker. Das Gesamtvolumen des Stabe bleibt dabei näherungsweise gleich – es verändert sich lediglich die Form.
Häufig kann bei der Berechnung der Querkontraktion auf die Anwendung des allgemeinen Hookeschen Gesetzes verzichtet werden, da sich die Änderung des Durchmessers proportional zu der relativen Änderung der Länge verhält. Man kann somit das vereinfachte Hookesche Gesetz zur Berechnung der Verformung in Querrichtung anwenden.
Bei der Berechnung dient uns die Poissonzahl, die auch als Querkontraktionszahl bezeichnet wird.
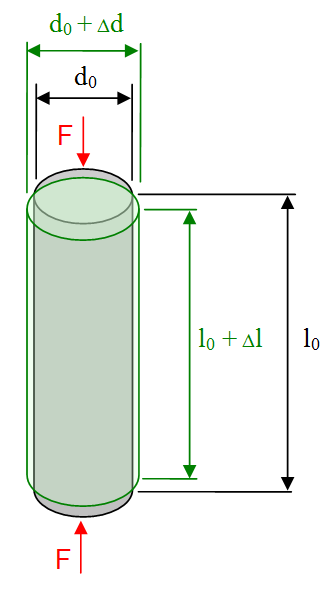
Darstellung der Verformung eines Stabes unter Drucklast
Berechnung der Spannung
Um die Verformung berechnen* zu können, muss man zunächst die vorliegende mechanische Spannung ermitteln. Dies wurde bereits in dieser vorhergehenden Aufgabe durchgeführt:
Die Berechnung in diesem Beispiel hat folgende Druckspannung ergeben:
σD = -167,2 N/mm2
Mit diesem Wert können wir weiterrechnen.
Berechnung der Verformung
a) Verformungen in Längsrichtung = Dehnung / Stauchung
Bei der Verformung in Längsrichtung handelt es sich in unserem Beispiel um eine Stauchung, da eine Druckkraft auf den Stab wirkt. Zur genauen Berechnung brauchen wir folgende Rechengrößen:
- Die Ausgangslänge des Stabes: l0 = 27 mm
- Den E-Modul des Werkstoffs: E = 2,1 · 105 N/mm2
(gleicher Werkstoff wie bei der Berechnung der Spannung) - Die Druckspannung: σD = -167,2 N/mm2
Mit diesen Werten berechnen wir die Verformung in Längsrichtung wie folgt:
ε = σD / E
ε = -167,2 N/mm2 / (2,1 · 105 N/mm2)
ε = -7,95 · 10-4
Längenänderung des Stabes berechnen
Die Dehnung bzw. Stauchung ε ist eine dimensionslose Größe. Wenn man die Stauchung in mm wissen möchte, spricht man von der Längenänderung ∆l. Die Längenänderung berechnet sich wie folgt:
Grundformel:
=> Längenänderung: ∆l = ε · l0
∆l = -7,95·10-4 · 27mm
∆l = -0,022 mm
=> Unser Stab wird also um 0,022mm kürzer.
b) Verformung in Querrichtung = Querkontraktion:
Der Längenänderung in Längsrichtung steht eine Breitenänderung in Querrichtung gegenüber. Der Stab wird dicker, da er durch die Druckkraft gestaucht wird. Um die Querkontraktion bzw. die Breitenänderung zu berechnen, benötigen wir folgende Größen:
- Die Ausgangsbreite des Stabes: d = 6mm
- Die Ausgangslänge des Stabes: l0 = 27 mm
- Längenänderung: ∆l = -0,022 mm
- Possionzahl Stahl: ʋ = 0,3
Die Änderung des Stab-Durchmessers berechnet sich nun wie folgt:
Grundformel der Poissonzahl:
=> Breitenänderung: Δd = - ʋ · (Δl/l) · d
Δd = -0,3 · (-0,022mm/27mm) · 6mm
Δd = 0,0015 mm
=> Unser Stab wird also um 0,0015mm breiter.



