Die Querkontraktion beschreibt die Verformung eines Bauteils quer zur Belastungsrichtung bei einer Zug oder Druckkraft.
Der Elastizitätsmodul beschreibt die Dehnung eines Materials in Richtung einer einwirkenden Kraft – das Material wird entweder gedehnt oder gestaucht. Eine Probe, die z.B. gezogen wird, verformt sich aber auch quer zur Wirkrichtung der auf sie einwirkenden Kraft. Dadurch bleibt das Volumen des Werkstücks - trotz der Dehnung in Längsrichtung - nahezu konstant. Dieser Effekt wird in der Festigkeitslehre Querkontraktionen genannt. Die Querkontraktion gehört demnach zu den Elastizitätskonstanten.
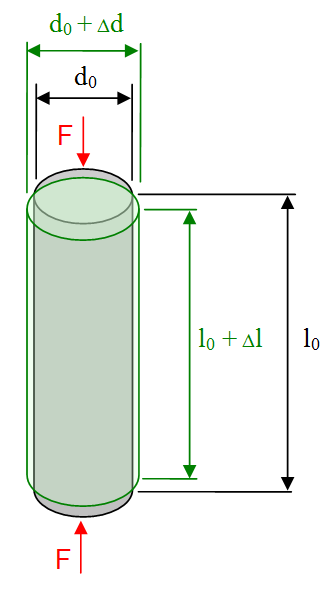
Darstellung der Verformung eines Stabes unter Drucklast
Dehnung = ∆l , Querkontraktion = ∆d
Um bei Berechnungen auf die komplizierte Anwendung des Hookeschen Gesetzes verzichten zu können, bedient man sich bei der Ermittlung der Querkontraktion einer Vereinfachung. Hierbei wird zuerst einmal vorausgesetzt, dass die Beziehungen zwischen den Spannungen und Dehnungen linear sind. Diese Beziehungen lassen sich in einer Matrix darstellen, wobei die wesentlichen Materialdaten die Querkontraktionszahl ʋ und das Elastizitätsmodul E sind.
Es besteht der folgende mathematische Zusammenhang zwischen Schubmodul G, Querkontraktionszahl ʋ und E-Modul E:
G - Schubmodul (N/m2)
E - E-Modul (N/m2)
K - Kompressionsmodul (N/m2)
ʋ - Poissonzahl (dimensionslos)
Berechnung der Querkontraktion
Die Querkontraktion kann man mit Hilfe der Poissonzahl (auch Querkontraktionszahl) berechnen. Die Poissonzahl ist eine Werkstoffkonstante und ist somit bekannt, insofern der Werkstoff* des betrachteten Bauteils bekannt ist.
=> Querkontraktion: Δd = - ʋ • (Δl/l) • d
ʋ - Poissonzahl / Querkontraktionszahl (dimensionslos)
d - Ursprungsdicke (m)
∆d - Dickenänderung (m)
l - Ursprungslänge (m)
∆l - Längenänderung (m)
Um die Querkontraktion mittels der oben genannten Formel berechnen zu können, muss man zunächst die Längsdehnung bzw. –stauchung Δl ermitteln.
Ein Beispiel für die Berechnung der Verformung unter Drucklast finden Sie hier: Verformung Berechnen - Beispiel
Querkontraktion - Beispiele
Die Querkontraktionszahl für Stahl liegt bei etwa 0,3, wobei sich der Wert bei Temperaturschwankungen kaum ändert. Auch die Querkontraktion anderer Werkstoffe*, wie Holz oder harte Kunststoffe bewegt sich im Wert zwischen 0,2 und 0,4. Sobald der Wert für die Querkontraktionszahl = 0,5 ist, ist das Material inkompressibel.
Bei Werten größer als 0,5 tritt bei Zugbelastung eine Abnahme des Volumens auf. Ein solches Verhalten können poröse Materialien oder auch Faserverbundwerkstoffe aufweisen.
Für die Ermittlung der Querkontraktionszahl dient der Zugversuch nach DIN EN ISO 527-1.



